Phase-field
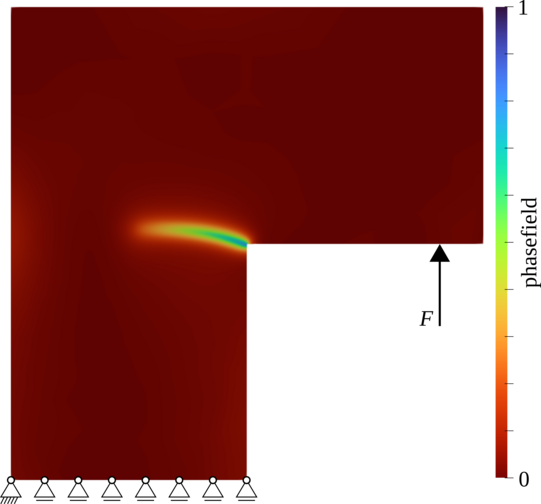
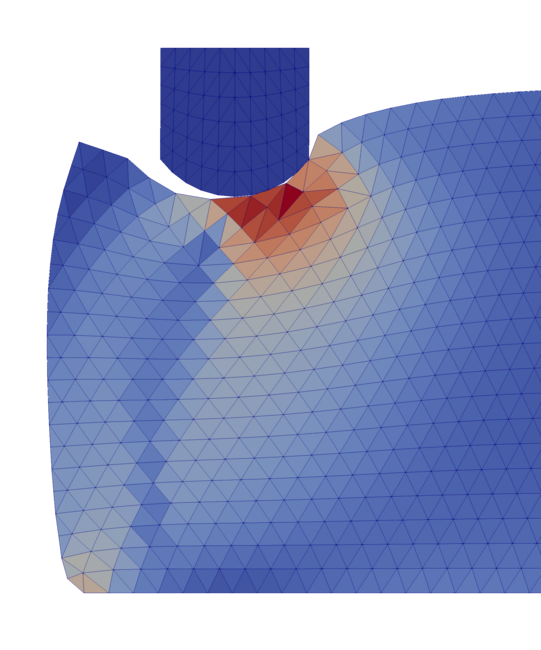
In material modeling, some problems require working with distinct states, i.e. non-continuous fields. Prime examples for this are fracture mechanics (ruptured vs. healthy components) and phase transformations (e.g. austenite vs. martensite). In contrast to continuous fields like temperature or displacements, non-continuous field entail significant challenges, like severely mesh-dependent solutions and numerical issues. In order to address those, an auxiliary continuous field, the so-called phase field, is introduced, which allows for the computation of regularized problems. It renders two-dimensional surfaces (like interfaces or fracture surfaces) into three-dimensional ones and accounts for the transitions (e.g. different levels of damage during fracture or phase mixtures) in space and time. Current research includes advanced algorithms for fracture and interface elasticity, as well as improving numerical stability and computational efficiency.
Contact: Hendrik Wilbuer
Multiscale Methods / Homogenization
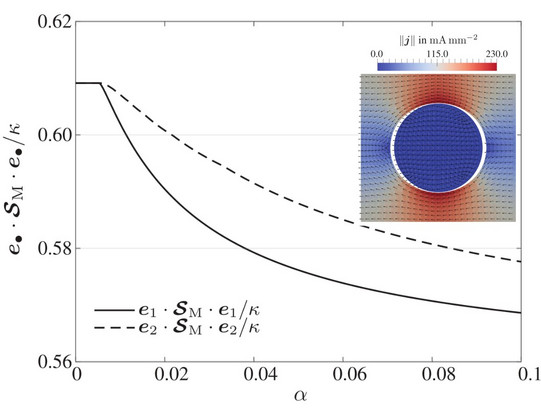
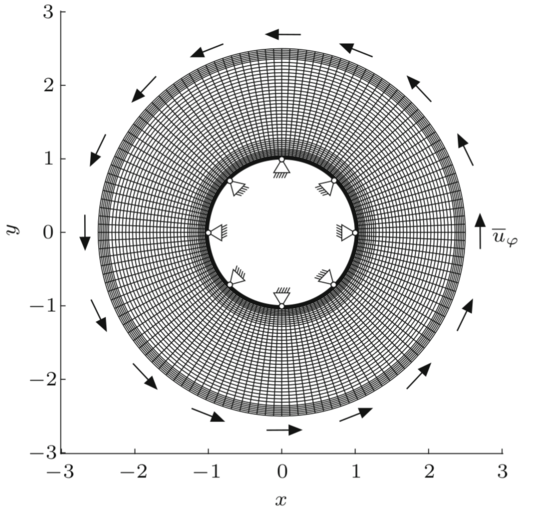
The effective material response observable at the macroscopic scale is a manifestation of the underlying material microstructure and of physical processes occurring at lower scales. While this microscale information is only implicitly taken into account in classic phenomenological material models, computational multiscale approaches explicitly use experimental microscale data to predict the effective response of materials. However, bridging at least two distinct length scales with multiscale methods is intrinsically associated with a significant computational burden. Against this background, research efforts at the Institute of Mechanics focus on the appropriate representation of microscale information in unit cells, on computational multiscale approaches for strongly coupled multiphysics problems and on state-of-the-art spectral solvers.
Contact: Tobias Kaiser
Neural Networks / Data Driven Mechanics
Neural Networks
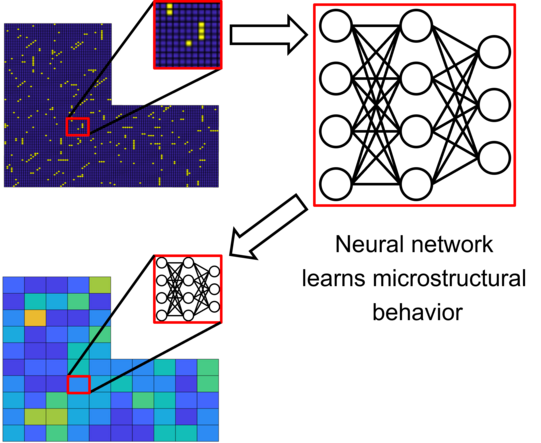
Neural networks are machine learning models inspired by the architecture and function of biological brains. They are capable of modeling complex systems and represent the state of the art in several applications, including image and video analysis, pattern recognition, natural language processing and generative modeling. In computational mechanics, neural networks are for example utilized as material models, to solve partial differential equations or for multiscale modeling. In these domains, they offer fast, efficient and flexible solutions compared to traditional methods, particularly for complex physical systems. However, they often fail to fulfill physical laws or constraints. Therefore, our research focuses on efficiently embedding physical information into neural networks.
Data-driven Mechanics
Data-driven mechanics is a cutting-edge approach in engineering that uses data to predict how materials and structures will behave. Instead of relying on complex mathematical models directly, scientists collect data from sophisticated simulations, like multiscale methods, to construct a data set. This data set is then used directly to solve engineering problems, without the need to resolve the complex mathematical models. This method is particularly useful for complex materials whose behaviors are hard to model and therefore result in time consuming numerical simulations. The research at the Instutite focusses on the application and extension of this method to path-dependent material behavior - including the use of neural networks.
Contact: Gian-Luca Geuken, Marius Harnisch
Isogeometric Analysis (IGA)
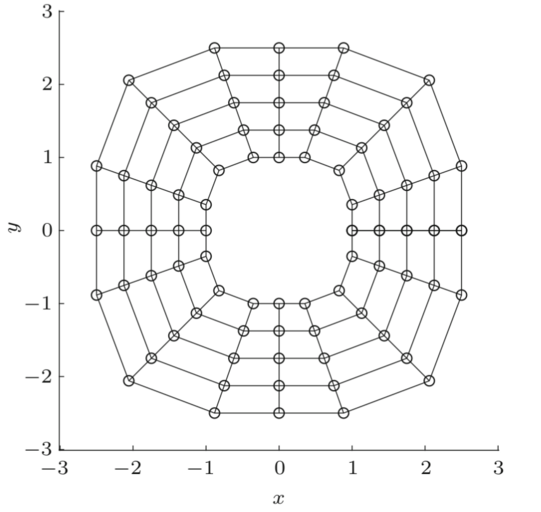
Isogeometric Analysis (IGA) has originally been developed with the aim to close the gap between computer-aided design (CAD) and finite element analysis (FEA). The most relevant difference between IGA and classic finite element approaches is the use of splines, respectively NURBS (non-uniform rational B-Splines) , as basis functions. This leads to additional advantages of IGA, such as an exact representation of the underlying geometry and a higher continuity within the entire computational domain. The latter enables, for example, to solve 4th-order PDEs with an IGA framework such as they occur in gradient elasticity.
Contact: Carina Witt
Particle Finite Element Method (PFEM)
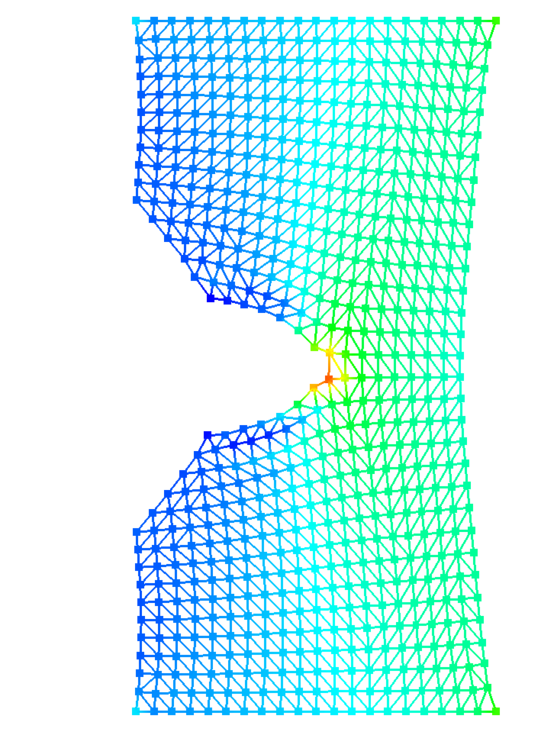
The Particle Finite Element Method (PFEM) is a class of numerical techniques that combines the strengths of the Finite Element Method (FEM) in the modelling of complex material behaviour with the topological flexibility of particle methods to address complex engineering problems. Originally developed for fluid simulation of free surface flows, the method is particularly useful for modelling problems involving large deformations and associated changes in the topology of a body, which are challenging for traditional FEM.
Contact: Markus Schewe
Computational Optimization
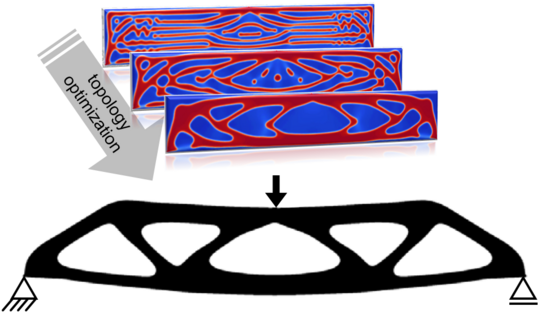
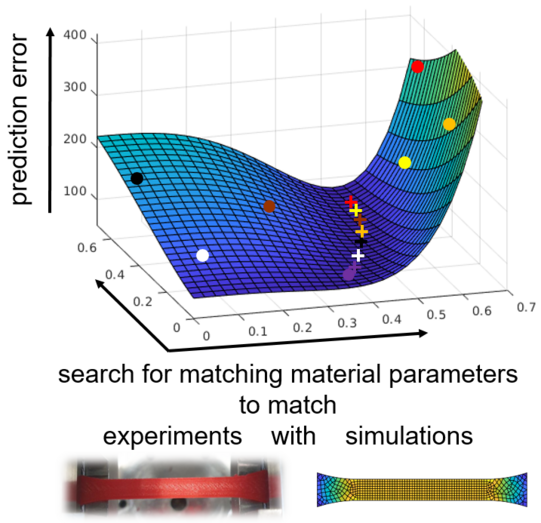
Computational optimization allows us to optimize structures or to find best fitting material parameters. What is best, depends on the application of interest and is recast into a mathematical optimization problem. The tools of computational optimization allow us, for instance, to search for a geometry with highest load-bearing capacity given a fixed amount of available material. They are also used to search for damage-mitigating load paths to prevent failure and for materials with exceptional sustainability or acoustic attenuation.
Contact: Patrick Kurzeja