Failure at Different Length and Time Scales
Failure in materials and structures can develop in different forms and can be driven by various mechanisms. Different time scales are relevant for the description of failure. The fracture of, for example, ceramic materials, occurs virtually instantaneously. However, the fatigue of, for example, metallic components, develops over many hundreds to hundreds of thousands of load cycles before macroscopic failure can be identified.
Damage
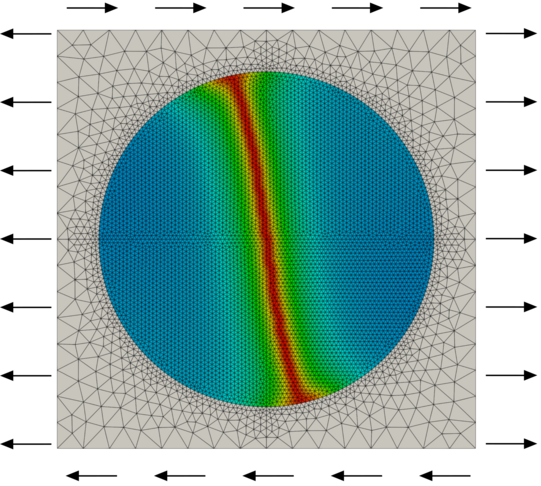
From the viewpoint of numerical models, the most common categories of damage are quasi-brittle damage and ductile damage. Quasi-brittle damage is associated with elastic deformation, whereas ductile damage involves plastic deformation of the material. Both forms of damage are represented in macroscopic material models by continuously increasing variables. These variables degrade the material's effective properties, most notably its stiffness. The resulting softening behavior leads to the localization of the damage zone, which can cause mesh-dependent simulation results. This problem can be mitigated by using methods such as gradient-based regularization.
Contact: Klas Feike
Fatigue
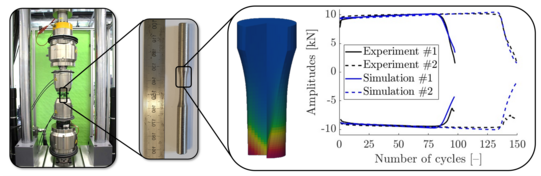
Modeling the fatigue behavior is essential for the prediction of a material's lifespan and for ensuring structural integrity. It enables engineers to design safer and more durable components, optimize material usage, and reduce maintenance costs, thereby enhancing the performance and reliability. Fatigue behavior is generally divided in low cylce fatigue and high cycle fatigue. Low cycle fatigue involves high stress amplitudes and plastic deformation (ductile damage) with fewer cycles to failure, while high cycle fatigue features low stress amplitudes, elastic deformations (brittle damage), and more cycles to failure. Depending on the underlying mechanisms, a suitable damage model is appropriately extended. On the one hand this enhancement includes criteria for modeling the fatigue-related material degradation, on the other hand it also includes methods for efficient computations.
Contact: Kai Langenfeld
Fracture
Fracture simulation in computational mechanics is crucial for predicting and preventing structural failures, ensuring the safety and longevity of engineering components. Simulating fracture is a challenging subject in research due to the complex behaviour of cracks, involving initiation and propagation, crack-branching and stress-localization as well as distinct behaviour for tension and compression acting on multiple length-scales. Earlier fracture models encounter difficulties in representing cracks with arbitrary and evolving geometries without predefining crack-paths or mesh-dependencies within the Finite-element method. Advanced methods such as the phase-field approach face challenges in achieving numerical stability and computational efficiency. Typical applications are prediction and optimization of fatigue and failure of macro- and microstructures and the coupling of fracture with other physical effects.
Contact: Felix Rörentrop, Henning Lammen
Plasticity at Different Scales
Macroscopic Models
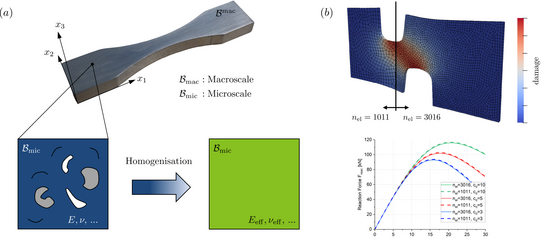
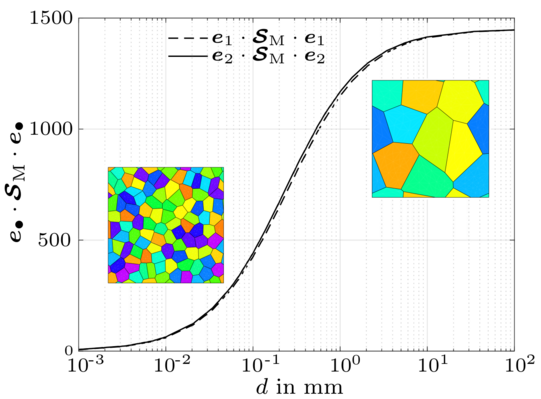
Macroscopic models predict material behaviour at the large scale by homogenising the heterogeneous microstructure, replacing a material with an equivalent homogeneous continuum that exhibits effective properties. While not explicitly accounting for microscopic features such as crystallographic defects, for example inclusions, voids, microcracks, or slip systems within individual grains, these models successfully predict a wide range of material responses under different loading conditions. Their computational efficiency allows for simulating full-scale components, making them invaluable for optimising the performance, safety, and durability of engineering designs. At our institute, we focus on developing macroscopic models to accurately predict complex material behaviours including plasticity, damage, fracture, phase transformations, and their coupling with thermal and electrical effects. To enhance the predictive capabilities of our models, we employ gradient-type regularisation techniques of, e.g., micromorphic type, to address challenges, such as mesh dependency and localisation.
Contact: Merlin Böddecker
Microscopic Models: Crystal Plasticity
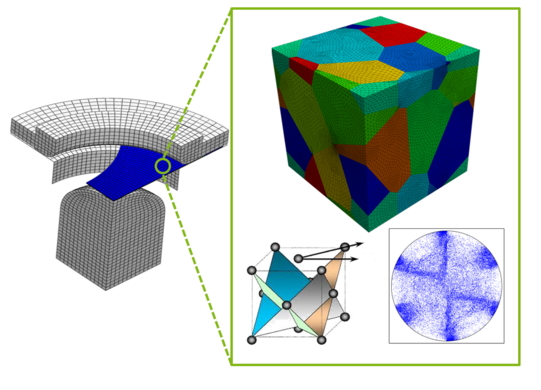
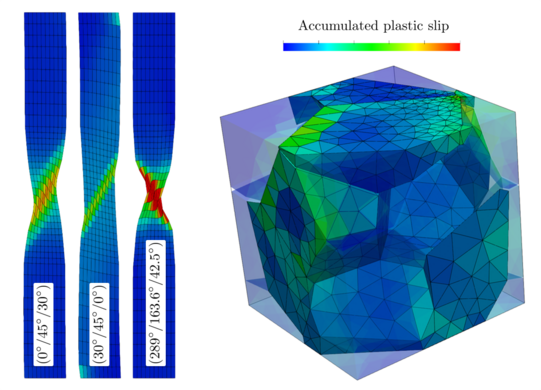
The macroscopic properties of polycrystalline materials are governed by deformation mechanisms at the microscopicscale. One such example are crystal plasticity models which incorporate the crystallographic slip systems of the underlying material into the constitutive model. It is assumed that plastic slip occurs only on distinct slip systems once a critical shear stress is exceeded yielding an anisotropic material response. The main numerical challenges are the selection of active slip systems and the computation of non-unique solutions. Furthermore, the basic framework may be extended to account for rate effects, gradient enhancement, dislocation densities, cross hardening, twinning and many more. Typical applications are the prediction of texture evolutions, micromechanical field distributions or strain localization.
Contact: Alexander Niehüser
Coupled Problems
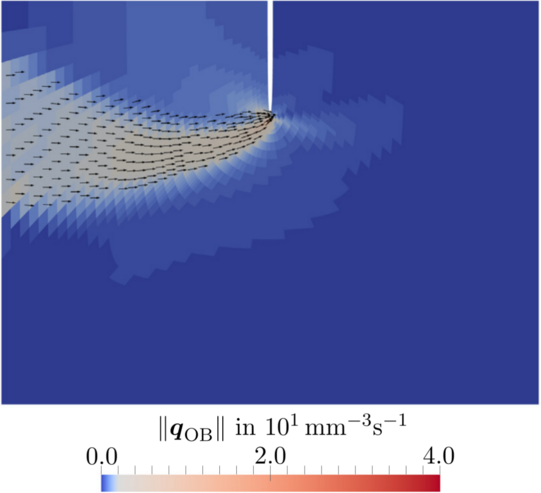
In many real-world scenarios, material behavior is not limited to a single physical phenomenon but involves the coupling of multiple fields, such as thermo-mechanics, (chemo-)electro-mechanics and electro-mechanics. As an example, the flow of electric current can generate heat, leading to thermal expansion and mechanical stress. To accurately capture these complex interactions, coupled multiphysics models are essential. These models consider the interplay between different physical fields, allowing for a more comprehensive understanding of material behavior under various conditions. By incorporating the coupling effects, these models enable the prediction of material response in a wide range of applications, from the design of electronic devices to the healing mechanisms of bone.
Contact: Dilek Güzel
Phase transformations
Shape Memory Alloys
(Magnetic) shape memory alloys (SMA) are fascinating materials. "Shape memory" means that the position of atoms of these alloys can change spontaneously under the influence of mechanical force, for example. However, further external influences, e.g. changes in temperature, cause the atoms to "jump" back to their original positions - they remember their previous position. In this way, entire structures and components can remember their original shape and return to it. Unfortunately, the complete behavior of SMA and in particular the adverse effects such as functional fatigue are not yet fully understood. Therefore, there is still a great need for research in this area in order to be able to realize the future-oriented possible applications of these alloys.
Bitte bestätigen Sie die Aktivierung dieses Videos.
Nach der Aktivierung werden Cookies gesetzt und Daten an YouTube (Google) übermittelt.
Zur Datenschutzerklärung von Google
Contact: Thorsten Bartel
Recovery and Recrystallization
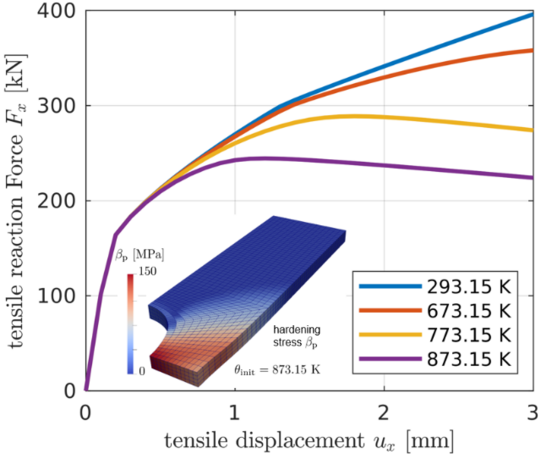
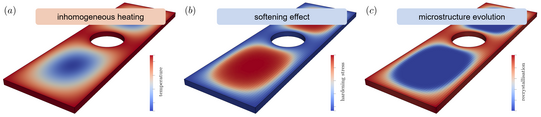
Recovery and recrystallisation are essential metallurgical processes that occur at elevated temperatures and significantly influence material properties of metals in the form of strength and ductility. These processes, driven by the accumulation of energy stored introduced by work hardening, involve the reduction of dislocation density by annihilation and rearrangement of dislocations (recovery) and the formation of new grains (recrystallisation). At our institute, we have developed a macroscopic model that unifies the effects of static and dynamic recovery and recrystallisation, as well as grain growth and refinement. By incorporating physically motivated evolution equations and adhering to thermodynamic principles, our model accurately predicts the complex interplay of these processes across various thermomechanical loading scenarios. This includes prediction of microstructural changes and their impact on material strength and ductility in hot forming and annealing processes.
Contact: Merlin Böddecker
Interfaces and Size Effects
The effective material response is inherently related to the underlying microstructure. Interfaces, such as phase/grain boundaries, significantly affect the overall response. These interfaces can act as barriers to various physical phenomena, such as the flow of the electric current. Different interface formulations such as elastic interface, cohesive interface, and generalised imperfect interface, are employed to simulate material behaviour accurately. Notably, the effect of interfaces varies with the size of the material under consideration. This phenomenon, known as the size effect, is particularly pronounced in materials with high surface-to-volume ratios like nanoparticles or materials with numerous grain boundaries. Understanding and predicting this size-dependent behavior is crucial for designing materials with tailored properties.
Contact: Dilek Güzel
Biomechanics
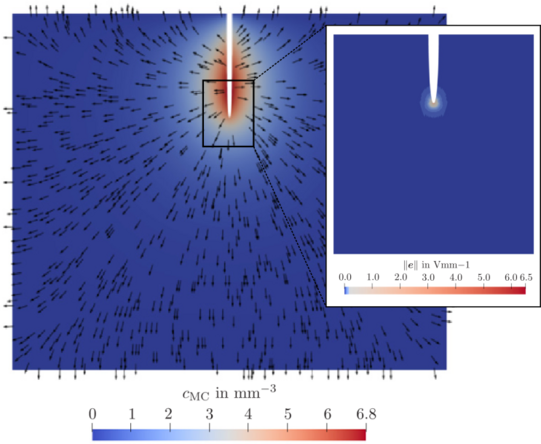
It has been found that bones exhibit flexoelectric properties, which means that they will polarise in response to an inhomogeneous strain field. This effect could play a significant role in the bone remodelling process. Since large strain gradients are present in the vicinity of microcracks within the bone structure, flexoelectricity occurs and initiates bone remodelling through the coupling with various cellular processes. In order to better understand this process and the role of flexoelectricity in bones, a modelling approach based on chemo-electro-mechanical coupling is developed. In numerical simulations, it can be used to simulate the electromechanical behaviour of bone together with the cellular processes which lead to the healing of microcracks.
Contact: Carina Witt